Stardust Crown
スクリーン上の3Dオブジェクトをポインティング・デバイス(マウスなど)で操作する方法について記述します。
基本的に三次元のものを完全な形で二次元に投影するのは難しいのですが、(実質的に2変数ですむ)回転に特化することで、かなり自然な対応を実現することができます。
物体を“形は変えずに”操作する(つまり物体を動かす)というのは、次の2つの組み合わせで表現できます。
平行移動というのは、ある1点Xを動かし、さらにその他の構成点とXとの相対位置を一定に保つ操作のことを言います。
2軸回転というのは、互いに平行でない2つのベクトルのいずれかを軸にとった物体の回転のことを言います。
もし注目する物体が1つだけで、適度な大きさならば、実用的には「移動」は必要ないでしょう。物体の初期位置を具合良く画面に納めるようにしておけばよいのですから。そのとき、その物体を「よく見る」ためには、回転だけできれば十分です。
このとき、回転軸は物体の中心点を通るようにしておくのが賢明でしょう。
ということで物体を自由に回転させればよい、というお話になるわけです。さらに、物体が1つであれば、実は物体はまったく動かさず、視点(と視線)を動かしても構いません。
したがって、操作に伴って見る側が動くと考えても差し支えはないのです。
では、どのように物体を回転させましょうか、というお話です。いま、ポインティング・デバイスで操作したいわけですから、まずは仮想空間上の点とスクリーン上の点との対応を考えることになります。
ところが、物体上の点を直接扱おうとするのは巧いやり方とはいえません。物体ごとにまちまちな、スクリーンの点と物体の点とを対応させるアルゴリズムが必要になるでしょうし、そのようなプログラムは複雑です。
よって、物体に触らずに操作することを考えます。そこで、物体がだいたい収まる球を持ち出しましょう。(一般には、スクリーンの中心の投影線と球の中心とを一致させ、画面が球面の輪郭に内接するようにすればよいです。)物体が球に対して固定されていると考えれば、(物体の形状に関わらず)球を操作することで物体を動かすことができます。(操作する部分は視点側の半球になります。)
そして、球は非常に扱いやすいオブジェクトですから、プログラムも書きやすいのです。
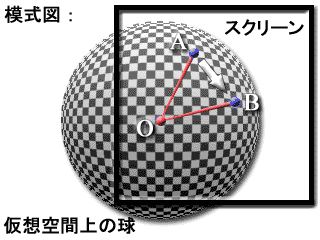
色々な手法があるのでしょうが、私が思いついたのは、ポインティング・デバイスでドラッグして操作する手法です。ドラッグ開始点Aがドラッグ終了点Bに重なるような回転を行うことにします。(あるいはドラッグ中、連続的に変化させてもよいでしょう。)

球の中心Oは既知ですし、(例えばスクリーン上の座標を仮想空間の xy 平面とを対応させれば)AおよびBを球上の点に対応させることは容易にできます。(ここでAおよびBは、スクリーン上の点であり、変換した仮想空間上の点でもあります。Oは仮想空間上の点です。)
回転軸φはOA×OB(OAベクトルとOBベクトルの外積)から、また、回転角θは−cosθ(とsinθ)がわかれば十分−OA・OB(OAベクトルとOBベクトルの内積)から求められます。
以上から、物体を回転軸φ、回転角θで回転させればよいわけです。
C++ および OpenGL を用いた例の一部です。
void vectorExterior(GLdouble* v1, GLdouble* v2, GLdouble* v3) {
v3[0] = v1[1] * v2[2] - v1[2] * v2[1]; // 外積ベクトル
v3[1] = v1[2] * v2[0] - v1[0] * v2[2];
v3[2] = v1[0] * v2[1] - v1[1] * v2[0];
vectorNormalize(v3[0], v3[1], v3[2]); // 正規化
};
GLdouble vectorCos(GLdouble* v1, GLdouble* v2) {
GLdouble cs = v1[0] * v2[0] + v1[1] * v2[1] + v1[2] * v2[2];
GLdouble stock = (v1[0] * v1[0] + v1[1] * v1[1] + v1[2] * v1[2]) * (v2[0] * v2[0] + v2[1] * v2[1] + v2[2] * v2[2]);
if (stock > 0) {
cs /= sqrt(stock); // 内積からもとめた cosθ
}
return cs;
};
void vectorNormalize(GLdouble& x, GLdouble& y, GLdouble& z) {
GLdouble r = x*x + y*y + z*z;
if (r > 0) {
x = x / sqrt(r);
y = y / sqrt(r);
z = z / sqrt(r);
}
};
void vectorRotation(GLdouble* v1, GLdouble* ax, GLdouble c) {
// v1 回転対象のベクトル ; ax 軸 ; c 角度(cos)
GLdouble s = sqrt(1-c*c);
GLdouble v2[3];
v2[0] = v1[0] * (c + (1-c) * ax[0] * ax[0]) + v1[1] * ((1-c) * ax[0] * ax[1] - ax[2] * s) + v1[2] * ((1-c) * ax[0] * ax[2] + ax[1] * s);
v2[1] = v1[0] * ((1-c) * ax[0] * ax[1] + ax[2] * s) + v1[1] * (c + (1-c) * ax[1] * ax[1]) + v1[2] * ((1-c) * ax[1] * ax[2] - ax[0] * s);
v2[2] = v1[0] * ((1-c) * ax[0] * ax[2] - ax[1] * s) + v1[1] * ((1-c) * ax[1] * ax[2] + ax[0] * s) + v1[2] * (c + (1-c) * ax[2] * ax[2]);
for (int i=0; i < 3; i++) {
v1[i] = v2[i];
}
};
※ポインティングデバイス(マウス)の指定座標は既に拾えているものとします。
void transRotate(GLint x1, GLint y1, GLint x2, GLint y2) {
// 開始点が (x1, y1) ,終了点が (x2, y2) となります
GLdouble p1[3]; GLdouble p2[3]; // マウス指定座標
GLdouble ax[3]; // 軸ベクトル
GLdouble q1[3]; GLdouble q2[3]; GLdouble up[3]; // 視点、原点、上方
GLdouble cs;
GLdouble sn; GLdouble stock; GLdouble r;
GLint i;
// 適当な縮尺をとります
r = radius * 3.0;
sn = GLdouble(glnWidth + glnHeight) * 0.25;
cs = GLdouble(glnWidth) * 0.5;
p1[0] = (GLdouble(x1) - cs) / sn * r; // 変換マウス座標1
p2[0] = (GLdouble(x2) - cs) / sn * r; // 変換マウス座標2
cs = GLdouble(glnHeight) * 0.5;
p1[1] = (cs - GLdouble(y1)) / sn * r;
p2[1] = (cs - GLdouble(y2)) / sn * r;
if ((stock = r*r - (p1[0] * p1[0]+p1[1] * p1[1])) >= 0) { // if (p1 on the earth ?)
p1[2] = sqrt(stock); // p1 決定
if ((stock = r*r - (p2[0] * p2[0]+p2[1] * p2[1])) >= 0) { // if (p2 on the earth ?)
p2[2] = sqrt(stock); // p2 決定
for (i=0; i < 3; i++) { // 視点ベクトル
q1[i] = LookFrom[i] - Op[i];
}
q2[0] = 0.0; q2[1] = 0.0; q2[2] = r; // ウィンドウ上での原点の座標
up[0] = 0.0; up[1] = 1.0; up[2] = 0.0; // ウィンドウ上での上方向
vectorExterior(q2, q1, ax); // ax =“原点”を視点に向かって回転させるときの軸となるベクトル
cs = vectorCos(q1, q2); // 視点ベクトルと“原点”ベクトルの為す角を調べる
vectorRotation(p1, ax, cs); // マウス座標1を修正(1/2)
vectorRotation(p2, ax, cs); // マウス座標2を修正(1/2)
vectorRotation(up, ax, cs); // 上方向ベクトルを修正
vectorExterior(up, LookUp, ax);
cs = vectorCos(LookUp, up); // ウィンドウ上方向ベクトルと実際の上方向ベクトルの為す角を調べる
vectorRotation(p1, ax, cs); // マウス座標1を修正(2/2)
vectorRotation(p2, ax, cs); // マウス座標2を修正(2/2)
vectorExterior(p2, p1, ax); // マウス座標の回転軸を取得
cs = vectorCos(p1, p2); // マウス座標の回転角を調べる
vectorRotation(q1, ax, cs); // 新たな視点ベクトル
vectorRotation(LookUp, ax, cs); // 新たな上方向ベクトル
for (i=0; i < 3; i++) {
LookFrom[i] = q1[i] + Op[i]; // 視点座標に戻す
}
// 結果は視点の修正として実現します(OpenGL 依存なので詳細は省略)
setViewPoint(LookFrom[0], LookFrom[1], LookFrom[2], LookUp[0], LookUp[1], LookUp[2]);
} // end if (p2 on the earth ?)
} // end if (p1 on the earth ?)
}
Windows 系ユーザの方は、SandPile2.5D をダウンロードすることで、上記コードを試すことができます。
著作・制作/永施 誠